Coucou,
En ce dernier jour de Volksfest (et sous un grand soleil, ils ont une chance incroyable avec la météo, ces Allemands), je vais tenter de vous expliquer mon raisonnement pour l'histoire des grandes roues. Vous pouvez retrouver l'énoncé ici...
Commençons avec une mauvaise nouvelle : je crois bien qu'en l'état, la réponse à la question est « non, on ne peut pas calculer la distance », il manque en effet une donnée.
On peut faire un petit schéma pour regarder tout ça.
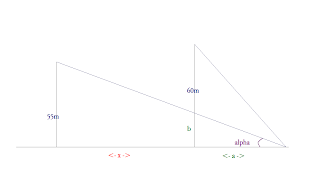Schéma que vous êtes fortement incités à agrandir pour y voir plus clair. On cherche x, et le problème, c'est que l'on ne connaît pas alpha. J'ai pris la liberté de considérer que le photographe était au niveau du sol, c'est une méchante approximation, mais on n'est de loin pas à ça près...
La photo nous permet de calculer b... D'après moi, la petite roue apparaît cinq fois plus petite que la grande... bref b serait donc 1/5 de 60 mètres, soit... 12 mètres.
On calcule ensuite tan(alpha) = opposé / adjacent si mes souvenirs sont exacts, soit b/a. On a aussi, et c'est ça qui est classe, tan(alpha) = 55/(x+a) si on se place dans l'autre triangle.
Donc... b/a = 55/(x+a). D'où l'on trouve que 55a donnent bx + ba. Ou encore bx = (55-b)a.
On a dit que b, c'était 12... Donc 12x = 43a, et on cherche x qui est donc... oui oui x = (43/12)a.
Bref, il nous faut une estimation de a... Que je n'ai pas vraiment... On va parier sur 200 mètres, ce qui est assez probable. On obtient alors x = 717 mètres ce qui n'est pas trop mal, on cherchait plutôt quelque chose dans les 800 mètres, mais entre l'erreur de mesure du rapport sur la photo et les approximations un peu partout, on peut s'estimer heureux.
Tout cela suppose que ma méthode est correcte, ce dont je doute assez, en fait. Vos remarques sont plus que bienvenues.
En ce dernier jour de Volksfest (et sous un grand soleil, ils ont une chance incroyable avec la météo, ces Allemands), je vais tenter de vous expliquer mon raisonnement pour l'histoire des grandes roues. Vous pouvez retrouver l'énoncé ici...
Commençons avec une mauvaise nouvelle : je crois bien qu'en l'état, la réponse à la question est « non, on ne peut pas calculer la distance », il manque en effet une donnée.
On peut faire un petit schéma pour regarder tout ça.
Schéma que vous êtes fortement incités à agrandir pour y voir plus clair. On cherche x, et le problème, c'est que l'on ne connaît pas alpha. J'ai pris la liberté de considérer que le photographe était au niveau du sol, c'est une méchante approximation, mais on n'est de loin pas à ça près...La photo nous permet de calculer b... D'après moi, la petite roue apparaît cinq fois plus petite que la grande... bref b serait donc 1/5 de 60 mètres, soit... 12 mètres.
On calcule ensuite tan(alpha) = opposé / adjacent si mes souvenirs sont exacts, soit b/a. On a aussi, et c'est ça qui est classe, tan(alpha) = 55/(x+a) si on se place dans l'autre triangle.
Donc... b/a = 55/(x+a). D'où l'on trouve que 55a donnent bx + ba. Ou encore bx = (55-b)a.
On a dit que b, c'était 12... Donc 12x = 43a, et on cherche x qui est donc... oui oui x = (43/12)a.
Bref, il nous faut une estimation de a... Que je n'ai pas vraiment... On va parier sur 200 mètres, ce qui est assez probable. On obtient alors x = 717 mètres ce qui n'est pas trop mal, on cherchait plutôt quelque chose dans les 800 mètres, mais entre l'erreur de mesure du rapport sur la photo et les approximations un peu partout, on peut s'estimer heureux.
Tout cela suppose que ma méthode est correcte, ce dont je doute assez, en fait. Vos remarques sont plus que bienvenues.
8 commentaires:
Bon ça m'embête cette histoire.
Pourtant j'étais persuadé qu'on avait assez de données avec les tailles réelles et relatives des deux grandes roues... Mais il faut croire que non. Pour l'instant je n'arrive pas à dire où c'est que tu as faux. Donc tu dois avoir raison.
Ça m'embête.
Bon, je ne m'avoue pas vaincu. Je trouverai la bonne distance avec ces 4 données. Même si je dois révolutionner toutes les mathématiques pour ça.
Et pourquoi dans le champ "heure" tu gardes "à l'adresse" au lieu de "à" ? Je ne sais pas d'où ça vient, erreur de traduction à mon avis, mais moi, je l'ai enlevée ;)
Coucou,
Je ne savais pas qu'on pouvait le corriger. C'est fait. Merci !
Je n'ai meme pas essayé de calculer, mais je me demande si l'optique de ton appareil photo intervient quelque part. Amuse-toi bien avec ton problème...
Coucou,
Il se pourrait que des informations sur l'objectif permettent de se passer de la distance entre le photographe et une des deux grandes roues pour finir le calcul. Mais je ne sais pas trop... Je m'y connais pas vraiment en objectifs.
Et sinon beh pour moi ke problème est un peu fini... Enfin si je poste ça sur mon blog c'est pour que les autres cherchent, pendant que je vais en cours ou que je dors... Ou que je me documente sur les Personas... Quelqu'un aurait un exemplaire du livre d'Alan Cooper chez lui ?
"Il se pourrait que des informations sur l'objectif permettent de se passer de la distance entre le photographe et une des deux grandes roues pour finir le calcul. Mais je ne sais pas trop... Je m'y connais pas vraiment en objectifs."
bah heu avcec les données exif (http://www.clubic.com/telecharger-fiche11174-exif-reader.html) tu auras la focale et tout ça, donc ça aide. J'imagine qu'il faut aussi compter la distortion, tout ça...
enfin en gros ça a l'air pas très très drôle, ce jeu.
En fait, je crois surtout que l'horizon est pas placé précisément, à cause des gens ; avec le diamètres des roues et pas leurs hauteurs, ça irait pas mieux?
Coucou,
La question n'est pas tellement de savoir quelles infos on peut avoir dans les métadonnées d'une photo (whaaa Windows en donne déjà tout plein d'ailleurs) mais surtout lesquelles pourraient éventuellement permettre de poursuivre le calcul, et comment ! Bon en tout cas ton message m'a donné envie de regarder et donc pour la photo des grandes roues, je peux vous annoncer que l'ouverture de lentille était F/5, de même que le Point-F, et que la longueur de la focale était 10 mm.
Pour la hauteur et le diamètre des grandes roues, j'ai considéré que c'était la même chose, ce qui est presque vrai en plus.
Ok, mais t'aurais une version non réduite de la photo? Parce que pour la roue du fond, je vois presque pas les bords...
Enregistrer un commentaire